How to Generate UML from Java (Round-Trip)?
Round-trip engineering is the ability to generate model from source code and generate source code from model, and keep them synchronized. You can make use of round-trip engineering to keep your implementation model and source code up-to-date, so as to produce up-to-date description on your model.
Generate/Update UML classes from code
You can produce UML classes from source code, or to update from code all the reversed UML classes in project. To do this:
- Select Tools > Code > Reverse Java Code... from the toolbar.
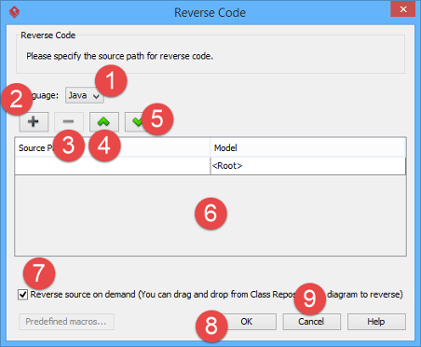
- In the Reverse Code dialog box, specify the mapping between source path and model. Model is a UML element that acts as a container of other elements. You can place the UML classes to be produced to specific model for better categorization. For example, you may create a Prototype model and an Implementation model for storing classes developed in prototype and implementation phrases respectively. Once a mapping is defined, round-trip engineering will be performed between the model and path as defined. You can add multiple Source-path-to-model mapping by pressing the + button. If you do not use model to structure your project, keep model to be <root>.

The mappings between source paths and model are defined - By default, an on-demand reverse engineering will be carried out, which means to form indexes to the added path(s) instead of actually reversing them. For details about on demand reverse engineering, refer to the section below. If you want to carry out actual reverse engineering, uncheck Reverse source on demand.
- Click OK to proceed with reversal.
Updating UML classes on a class diagram from code
Once you have performed round-trip engineering for once, you can update UML class(es) on a diagram from source code for reflecting the changes made in code. To update, right click on the background of the class diagram for update and select Utilities > Java Round-trip > Reverse Code from the popup menu.
| NOTE: | In order to trigger this function, make sure you have performed round-trip engineering at least for once and the diagram has at least one class. |
Updating specific UML classes from code
Once you have performed round-trip engineering for once, you can update specific UML class(es) from source code for reflecting the changes made on that particular class(es) To update, select in class diagram the UML class(es) you want to update. Right click on them and select Java Round-trip > Reverse Code from the popup menu.
An overview of Reverse Code dialog box
 |
| An overview of Reverse Code dialog box |
|
||||||||||||||||||||||||||||||
| A description of Reverse Code dialog box |
On-demand reverse engineering
Consider if you have a project that contains million of Java source file, and now you want to re-develop just a few classes in it. If you try to reverse the whole project it will take you a long time to complete the reverse due to the amount of classes (and relationships) are just too many. With on-demand reverse engineering, you will reverse the sources as indexes, and obtain an index tree in class repository. No actual UML classes will be reversed until you trigger the reverse manually. This reduces the processing time significantly.
To perform on-demand reverse engineering, make sure the option Reverse source on demand is checked in the Reverse Code dialog box.
 |
| The option Reverse source on demand that appear in reverse dialog box |
When finished reverse, you can lookup the index tree in class repository. Then, right click on the class you want to reverse and select Reverse Resources to where Resources are the classes you have selected, and select either New Class Diagram or Class Repository from popup menu. Both options will result in reversing the selection to UML classes, while the option New Class Diagram will create a class diagram and place the classes in it.
 |
| Reverse a java source file from index tree |
Related Resources
The following resources may help you learn more about the topic discussed in this page.
| 1. Generate or Update Java code from UML classes | Table of Contents | Chapter 4. C++ Round-trip |
